Graph Basics

GRAPH:

A graph is a non-linear data structure consisting of vertices (also known as nodes) and edges (links between vertices). Usually, this is denoted as G = <V, E>, where V is a set of vertices, and E is a set of edges. Each edge is a pair(x,y), where x and y belong to V. If the edge pair is ordered, the edge is called directed and thus the graph is directed graph. Otherwise, the graph is called undirected. Sometimes, an edge has a component called edge cost (or weight). Graphs have applications in many areas: a city map, airports, computer networks, electrical circuits, and so on.

A graph is simple if there is no more than one edge between any two vertices. Otherwise, a graph is called a multigraph. We also assume that a graph has no loops - an edge connecting the same vertex. I this course we will consider only simple graphs, without self-loops or multiple edges.

In a directed graph, an edge leaves its origin and ends in the destination. The out-degree of a vertex is the number of edges leaving the vertex. The in-degree of a vertex is the number of edges entering the vertex. The degree of a vertex is the number of edges entering and leaving the vertex. In the above example, the vertex v5 has the in-degree = 2, and the out-degree = 1, thus the degree is 3. The sink is a node, which has out-degree 0. A path is a sequence of distinctive vertices connected by edges. The path length is the number of edges on the path. In the weighted graph, the length is the sum of the costs along the path. A cycle in a directed graph is a path that begins and ends at the same vertex. A forest is a graph without cycles. A graph is connected if there is a path between any two vertices. A tree is a connected graph without cycles. An alternative definition, a tree is a connected forest.

PROPOSITIONS:

1. In a directed graph, the sum of in-degrees (or out-degrees) is equal to the number of edges. Reasoning: In a directed graph, any edge (x, y) contributes one unit to all in-degrees and one unit to all outdegrees.

2. In a connected graph with m edges, the sum of degrees of all vertices is 2*m. Reasoning: The proposition follows from the previous one.

3. In an undirected graph with n vertices, there are at most n*(n-1)/2 edges. In a directed graph with n vertices, there are at most n*(n-1) edges. Reasoning: Consider an undirected graph with n vertices and choose any vertex. The possible number of edges leaving this vertex is n-1. Take another vertex. The possible number of edges leaving this vertex is n-2 (don't count the edge between these vertices twice!), and so on. We have (n-1) + (n-2) + ... + 1 = n(n-1)/2

For all graphs, the number of edges and vertices satisfies the following inequality |E|<|V|^2, meaning that the number of edges is always less than the number of vertices squared. If the number of edges is close to |V|^2, we say that this is a dense graph, it has a large number of edges. Otherwise, this is a sparse graph. In most cases, the graph is relatively sparse.

4. Let G be an undirected graph :

If G is connected, then |E| >= |V|-1

If G is a tree, then |E| = |V|-1

If G is a forest, then |E| <= |V|-1

A complete graph is a graph in which every vertex is adjacent (i.e., connected) to every other vertex.

A subgraph of a graph G is a graph whose vertices and edges are subsets of the vertices and edges of G. If a graph is not connected, its maximal connected subgraphs are called connected components.

A spanning tree of a graph is a subgraph, which is a tree and contains all vertices of the graph.

APPLICATIONS OF GRAPHS:

• Representing relationships between components in electronic circuits
• Transportation networks: Highway network, Flight network
• Computer networks: Local area network, Internet, Web
• Databases: For representing ER (Entity Relationship) diagrams in databases, for representing dependency of tables in databases

REPRESENTATION:

To manipulate graphs we need to represent them in some useful form. Basically, there are three ways of doing this:

• Adjacency Matrix
• Adjacency List
• Adjacency Set

Graph Declaration for Adjacency Matrix 

First, let us look at the components of the graph data structure. To represent graphs, we need the number of vertices, the number of edges, and also their interconnections. So, the graph can be declared as:

Description

In this method, we use a matrix with size V × V. The values of the matrix are boolean. Let us assume the matrix is Adj. The value Adj[u, v] is set to 1 if there is an edge from vertex u to vertex v and 0 otherwise. In the matrix, each edge is represented by two bits for undirected graphs. That means an edge from u to v is represented by 1 value in both Adj[u,v ] and Adj[u,v]. 

To save time, we can process only half of this symmetric matrix. Also, we can assume that there is an “edge” from each vertex to itself. So, Adj[u, u] is set to 1 for all vertices. If the graph is a directed graph then we need to mark only one entry in the adjacency matrix.

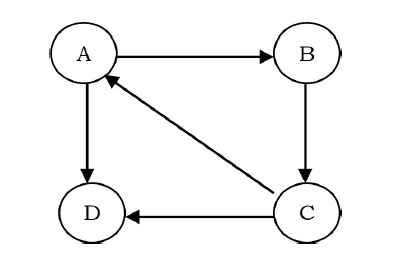
As an example, consider the directed graph below.

The adjacency matrix for this graph can be given as:

The adjacency matrix representation is good if the graphs are dense. The matrix requires O(V^2) bits of storage and O(V^2) time for initialization. If the number of edges is proportional to V^2, then there is no problem because V^2 steps are required to read the edges. If the graph is sparse, the initialization of the matrix dominates the running time of the algorithm as it takes O(V^2).

Graph Declaration for Adjacency List:

In this representation all the vertices connected to a vertex v are listed on an adjacency list for that vertex v. This can be easily implemented with linked lists. That means, for each vertex v we use a linked list and list nodes represent the connections between v and other vertices to which v has an edge. The total number of linked lists is equal to the number of vertices in the graph. Considering the same example as that of the adjacency matrix, the adjacency list representation can be given as shown above. Since vertex A has an edge for B and D, we have added them in the adjacency list for A. Same is the case with other vertices as well. 

For this representation, the order of edges in the input is important. This is because they determine the order of the vertices on the adjacency lists. The same graph can be represented in many different ways in an adjacency list. The order in which edges appear on the adjacency list affects the order in which edges are processed by algorithms.

Disadvantages of Adjacency Lists 

Using adjacency list representation we cannot perform some operations efficiently. As an example, consider the case of deleting a node. In adjacency list representation, it is not enough if we simply delete a node from the list representation, if we delete a node from the adjacency list then that is enough. For each node on the adjacency list of that node specifies another vertex. We need to search other nodes linked list also for deleting it. This problem can be solved by linking the two list nodes that correspond to a particular edge and making the adjacency lists doubly linked. But all these extra links are risky to process.

Graph Declaration for Adjacency Set:

It is very much similar to the adjacency list but instead of using Linked lists, Disjoint Sets [Union-Find] is used.

Comparison of Graph Representations

Directed and undirected graphs are represented with the same structures. For directed graphs, everything is the same, except that each edge is represented just once. An edge from x to y is represented by a 1 value in Adj[x][y] in the adjacency matrix, or by adding y on x’s adjacency list. For weighted graphs, everything is the same, except filling the adjacency matrix with weights instead of boolean values.